La derivada representa cómo una función cambia a medida que su entrada cambia.
Surge al asociar una línea recta con una línea curva, líneas que tienen con común dos puntos.
El proceso de encontrar una derivada es llamado diferenciación. El teorema fundamental del cálculo dice que la diferenciación es el proceso inverso de la integración en funciones continuas.
Supongamos que tenemos una función y la llamamos f. La derivada de f es otra función que llamaremos f'.
f'(x) representa la pendiente de la recta tangente a la gráfica de f en el punto x.
Existen diversas formas para nombrar a la derivada. Si f es una función, se escribe la derivada de la función f respecto al valor x en varios modos:
* Notación de Lagrange: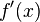 
-> se lee "efe prima de equis"
* Notación de Cauchy: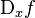 
y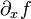 
-> se lee "d sub x de f", y los símbolos D y d deben entenderse como operadores.
*Notación de Leibniz: 
, 
y 
-> se lee "derivada de y (f ó f de x) con respecto a x".
La notación más simple para diferenciación, en uso actual, es debida a Lagrange. Para identificar las derivadas de f en el punto a, se escribe:
para la primera derivada,
para la segunda derivada,
para la tercera derivada,
para la enésima derivada (n > 3). (También se pueden usar números romanos).
sigue escribiendo porfavor :)
ResponderEliminar