LAGRANGE

Joseph Louis Lagrange (25 de Enero de 1736 - 10 de Abril de 1813), fue un matemático, físico y astrónomo italiano que después vivió en Prusia y Francia.
Lagrange elabora la teoría de las variaciones y efectúa interesantes hallazgos en las integrales elípticas y en los métodos de interpolación. Por otra parte, también contribuye al desarrollo de la mecánica y las funciones analíticas.
Si f(x) es continua en el intervalo cerrado [a,b] y derivable en todo punto del intervalo abierto (a,b), entonces existe al menos un punto c donde f'(c) = (f(b) - f(a))/(b - a).
H) f(x) es continua en [a,b]
f(x) es derivable en (a,b)
T) Existe c perteneciente a (a,b) /f'(c)=(f(b) - f(a))/(b - a)
H) f(x) es continua en [a,b]
f(x) es derivable en (a,b)
T) Existe c perteneciente a (a,b) /
CAUCHY

Augustin Louis Cauchy (21 de Agosto de 1789 - 23 de Mayo de 1857), fue pionero en el análisis matemático y la teoría de grupos de permutaciones, contribuyendo de manera medular a su desarrollo. También investigó la convergencia y la divergencia de las series infinitas, ecuaciones diferenciales, determinantes, probabilidad y física matemática.
Cauchy resolvió el problema de Poinsot, generalización del teorema de Euler sobre los poliedros. Publicaró una memoria sobre el cálculo de las funciones simétricas y el número de valores que una función puede adquirir cuando se permutan de todas las maneras posibles las cantidades que encierra. En 1814, apareció su memoria fundamental sobre las integrales definidas y luego abordando el teorema de Fermat sobre los números poligonales.
H) f(x) y g(x) continuas en [a,b]
f(x) y g(x) derivables en (a,b)
f'2(x) + g'2(x) distinto de 0 para todo x perteneciente a (a,b)
(Las derivadas no se anulan en el mismo punto del intervalo.)
g(a) distinto de g(b)
T) Existe c perteneciente a (a,b) /(f(b) - f(a))/(g(b) - g(a)) = f'(c)/g'(c)
f(x) y g(x) derivables en (a,b)
f'2(x) + g'2(x) distinto de 0 para todo x perteneciente a (a,b)
(Las derivadas no se anulan en el mismo punto del intervalo.)
g(a) distinto de g(b)
T) Existe c perteneciente a (a,b) /
LEIBNIZ

Gottfried Wilhelm von Leibniz (1 de Julio de 1646 - 14 de Noviembre de 17169), fue un filósofo, matemático, jurista, bibliotecario y político alemán.
Descubrió el sistema binario, fundamento de virtualmente todas las arquitecturas de las computadoras actuales.
Leibniz fue el primero, en 1692 y 1694, en emplearlas explícitamente para denotar alguno de los varios conceptos geométricos derivados de una curva, tales como abscisa, ordenada, tangente, cuerda y perpendicular.
Leibniz fue el primero, en 1692 y 1694, en emplearlas explícitamente para denotar alguno de los varios conceptos geométricos derivados de una curva, tales como abscisa, ordenada, tangente, cuerda y perpendicular.
En esta notación se representa la operación de diferenciar mediante el operador 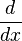 , es decir, la operación "derivada de la función f respecto de x" se representaría de este modo
, es decir, la operación "derivada de la función f respecto de x" se representaría de este modo 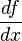 como un cociente de diferenciales. La belleza y utilidad de esta notación consiste en que permite recordar intuitivamente varios conceptos básicos del cálculo tales como la regla de la cadena, que con esta notación parece obvia debido a la cancelación de diferenciales (a pesar de que este razonamiento es incorrecto)
como un cociente de diferenciales. La belleza y utilidad de esta notación consiste en que permite recordar intuitivamente varios conceptos básicos del cálculo tales como la regla de la cadena, que con esta notación parece obvia debido a la cancelación de diferenciales (a pesar de que este razonamiento es incorrecto)  ; o bien el concepto de separación de variables en la resolución de ecuaciones diferenciales
; o bien el concepto de separación de variables en la resolución de ecuaciones diferenciales 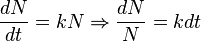 .
.
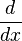 , es decir, la operación "derivada de la función f respecto de x" se representaría de este modo
, es decir, la operación "derivada de la función f respecto de x" se representaría de este modo 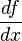 como un cociente de diferenciales. La belleza y utilidad de esta notación consiste en que permite recordar intuitivamente varios conceptos básicos del cálculo tales como la regla de la cadena, que con esta notación parece obvia debido a la cancelación de diferenciales (a pesar de que este razonamiento es incorrecto)
como un cociente de diferenciales. La belleza y utilidad de esta notación consiste en que permite recordar intuitivamente varios conceptos básicos del cálculo tales como la regla de la cadena, que con esta notación parece obvia debido a la cancelación de diferenciales (a pesar de que este razonamiento es incorrecto)  ; o bien el concepto de separación de variables en la resolución de ecuaciones diferenciales
; o bien el concepto de separación de variables en la resolución de ecuaciones diferenciales 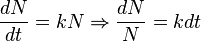 .
.La notación de Leibniz también es especialmente útil cuando se trabaja con derivadas parciales de funciones multivariables y sus operadores derivados, ya que indica en cada momento la variable de la función que se considera independiente, dejando el resto de variables como constantes en lo que se refiere a la derivación parcial.

No hay comentarios:
Publicar un comentario