

 Ejemplo:
Ejemplo:

 Ejemplo:
Ejemplo: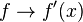

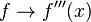
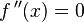
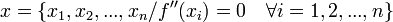
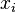 sustituyendo la variable dependiente en la función.
sustituyendo la variable dependiente en la función.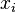 .
.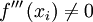 , se tiene un punto de inflexión en
, se tiene un punto de inflexión en 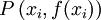 .
.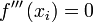 , debemos sustituir
, debemos sustituir 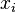 en las sucesivas derivadas hasta sea distinto de cero. Cuando se halle la derivada para la que no sea nulo, hay que ver qué derivada es:
en las sucesivas derivadas hasta sea distinto de cero. Cuando se halle la derivada para la que no sea nulo, hay que ver qué derivada es:Los puntos críticos permiten determinar los valores máximos o valores mínimos que alcanza la función. El punto crítico que se encuentra en el intervalo de una concavidad que abre hacia abajo permite determinar el valor máximo que alcanza la función y el que se encuentra en una concavidad que abre hacia arriba, al mínimo que alcanza la función.
Criterio de la primera derivada:
•Se determinan los intervalos de crecimiento y decrecimiento.
•Existe máximo relativo en los puntos en que la función pasa de creciente a decreciente.
•Existe mínimo relativo en los puntos en que pasa de decreciente a creciente.
Criterio de la segunda derivada:
•Calculamos la primera derivada, la igualamos a cero y resolvemos la ecuación resultante.
•Hallamos la segunda derivada.
•Las raíces de la ecuación obtenida se sustituyen en la segunda derivada.
•Si el resultado obtenido es positivo existe mínimo y si es negativo máximo.
Crecimiento y decrecimiento.
Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto:
*Una función f(x) es creciente en un punto a, si su derivada es positiva
*Una función f(x) es decreciente en un punto a, si su derivada es negativa.
Se procede de la siguiente forma:
• Se halla la derivada, se iguala a cero y se resuelve la ecuación resultante
• Con los puntos en los que se anula la derivada dividimos el dominio en intervalos.
• Se estudia el signo de la derivada en un punto cualquiera de cada uno de los intervalos resultantes.
Punto máximo -> creciente-decreciente: En ese valor de x donde f'(x)=0, hay un máximo.
Punto mínimo -> decreciente-creciente: En ese valor de x donde f'(X)=0, hay un mínimo.
Los máximos y mínimos son puntos que necesitan las dos coordenadas (x , y)
Para calcular la coordenada "y" de los máximos y mínimos, sustituimos el valor de x en la función.
Ejemplo:
f(x)= 1/4x^4 - 2x^2
-Obtenemos primera derivada:
f'(x)= x^3-4x
-Igualamos f'(x)= 0 para obtener puntos criticos
x^3 -4x= 0
x(x^2-4)= 0
x= 0 y x = +2/-2
-Nuestros puntos criticos serán 0,-2,+2
-Ahora obtenemos la segunda derivada
f''(x)= 3x^2-4
-Evaluamos los puntos criticos en la segunda derivada
f''(0)= -4 -> por lo tanto hay un máximo en x= 0
f''(-2)= 8 ->por lo tanto hay un mínimo en x= -2
f''(+2)= 8 -> por lo tanto hay un minimo en x= +2
-Los puntos de inflexion se obtienen igualando a cero la segunda derivada f''(x)= 0
3x^2-4=0
-Nuestros puntos de inflexión serán +raiz4/3 y -raiz4/3
concava hacia arriba (-ºº, -raiz4/3)U(+raiz4/3, +ºº)
concava hacia abajo (-raiz4/3, +raiz4/3)
2- Para la función identidad f(x)=x :
Si f(x)=x, su derivada es f'(x)=1
Ejemplo:
Si f(x)=x, su derivada es f'(x)=1
3- Para una constante "a" por una variable "x"
Si f(x)=ax, su derivada es f'(x)=a
Ejemplo:
Si f(x)=14x, su derivada es f'(x)=14
4- Para una variable "x" elevada a una potencia "n"
Si f(x)=xⁿ, su derivada es f'(x)= nxⁿˉ¹
Ejemplo:
Si f(x)= x², su derivada es f'(x)= 2x
5- Para una constante "a" por una variable "x" elevada a una potencia "n"
Si f(x)= axⁿ su derivada es f'(x)= anxⁿˉ¹
Ejemplo:
Si f(x) = 9x², su derivada es f'(x)= 18x
6- Para una suma de funciones:
Si f(x) = u(x) +v(x), su derivada es f '(x) = u'(x) + v'(x)
Ejemplo:
Si f(x)= 7x²+3x, su derivada es f'(x) = 14x+3



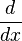 , es decir, la operación "derivada de la función f respecto de x" se representaría de este modo
, es decir, la operación "derivada de la función f respecto de x" se representaría de este modo 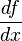 como un cociente de diferenciales. La belleza y utilidad de esta notación consiste en que permite recordar intuitivamente varios conceptos básicos del cálculo tales como la regla de la cadena, que con esta notación parece obvia debido a la cancelación de diferenciales (a pesar de que este razonamiento es incorrecto)
como un cociente de diferenciales. La belleza y utilidad de esta notación consiste en que permite recordar intuitivamente varios conceptos básicos del cálculo tales como la regla de la cadena, que con esta notación parece obvia debido a la cancelación de diferenciales (a pesar de que este razonamiento es incorrecto)  ; o bien el concepto de separación de variables en la resolución de ecuaciones diferenciales
; o bien el concepto de separación de variables en la resolución de ecuaciones diferenciales 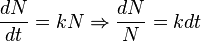 .
.
Supongamos que tenemos una función y la llamamos f. La derivada de f es otra función que llamaremos f'.
f'(x) representa la pendiente de la recta tangente a la gráfica de f en el punto x.
Existen diversas formas para nombrar a la derivada. Si f es una función, se escribe la derivada de la función f respecto al valor x en varios modos:
* Notación de Lagrange: 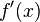 -> se lee "efe prima de equis"
-> se lee "efe prima de equis"
* Notación de Cauchy: 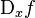 y
y 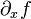 -> se lee "d sub x de f", y los símbolos D y d deben entenderse como operadores.
-> se lee "d sub x de f", y los símbolos D y d deben entenderse como operadores.
*Notación de Leibniz:  ,
,  y
y  -> se lee "derivada de y (f ó f de x) con respecto a x".
-> se lee "derivada de y (f ó f de x) con respecto a x".
La notación más simple para diferenciación, en uso actual, es debida a Lagrange. Para identificar las derivadas de f en el punto a, se escribe:
 para la primera derivada,
para la primera derivada, para la segunda derivada,
para la segunda derivada, para la tercera derivada,
para la tercera derivada, para la enésima derivada (n > 3). (También se pueden usar números romanos).
para la enésima derivada (n > 3). (También se pueden usar números romanos).